
Fig. 1 - Fricción estática: no se inicia el movimiento si la fuerza tangencial aplicada
Thace que el ángulo sea menor a φ
0 (no supera a
Fr).
Se define como fuerza de rozamiento o fuerza de fricción, a la fuerza entre dos superficies en contacto, a aquella que se opone al movimiento entre ambas superficies (fuerza de fricción dinámica) o a la fuerza que se opone al inicio del deslizamiento (fuerza de fricción estática). Se genera debido a las imperfecciones, mayormente microscópicas, entre las superficies en contacto. Estas imperfecciones hacen que la fuerza perpendicular R entre ambas superficies no lo sea perfectamente, si no que forme un ángulo φ con la normal N (el ángulo de rozamiento). Por tanto, la fuerza resultante se compone de la fuerza normal N (perpendicular a las superficies en contacto) y de la fuerza de rozamiento F, paralela a las superficies en contacto.
Rozamiento entre superficies de dos sólidos[editar]
En el rozamiento entre dos cuerpos se ha observado los siguientes hechos:
- La fuerza de rozamiento tiene dirección paralela a la superficie de apoyo.
- El coeficiente de rozamiento depende exclusivamente de la naturaleza de los cuerpos en contacto, así como del estado en que se encuentren sus superficies.
- La fuerza máxima de rozamiento es directamente proporcional a la fuerza normal que actúa entre las superficies de contacto.
- Para un mismo par de cuerpos (superficies de contacto), el rozamiento es mayor un instante antes de que comience el movimiento que cuando ya ha comenzado (estático Vs. cinético).
El rozamiento puede variar en una medida mucho menor debido a otros factores:
- El coeficiente de rozamiento es prácticamente independiente del área de las superficies de contacto.
- El coeficiente de rozamiento cinético es prácticamente independiente de la velocidad relativa entre los móviles.
- La fuerza de rozamiento puede aumentar ligeramente si los cuerpos llevan mucho tiempo sin moverse uno respecto del otro ya que pueden sufriratascamiento entre sí.
Algunos autores
sintetizan las leyes del comportamiento de la fricción en los siguientes dos postulados básicos:
1
- La resistencia al deslizamiento tangencial entre dos cuerpos es proporcional a la fuerza normal ejercida entre los mismos.
- La resistencia al deslizamiento tangencial entre dos cuerpos es independiente de las dimensiones de contacto entre ambos.
La segunda ley puede ilustrarse arrastrando un bloque sobre una superficie plana. La fuerza de arrastre será la misma aunque el bloque descanse sobre la cara ancha o sobre un borde más angosto. Estas leyes fueron establecidas primeramente por
Leonardo da Vinci al final del siglo XV, olvidándose después durante largo tiempo; posteriormente fueron
redescubiertas por el ingeniero francés Amontons en 1699. Frecuentemente se les denomina también leyes de Amontons.
Tipos de fricción[editar]

Fig. 2 - Diagrama de fuerzas para el esquema de la figura 1. Según sea la magnitud del empuje
T habrá fricción estática (equilibrio) o cinética (con movimiento).
Existen dos tipos de rozamiento o fricción, la
fricción estática (FE) y la
fricción dinámica (FD). El primero es la resistencia que se debe superar para poner en movimiento un cuerpo con respecto a otro que se encuentra en contacto. El segundo, es la resistencia, de magnitud considerada constante, que se opone al movimiento pero una vez que éste ya comenzó. En resumen, lo que diferencia a un roce con el otro, es que el estático actúa cuando los cuerpos están en reposo relativo en tanto que el dinámico lo hace cuando ya están en movimiento.
La fuerza de fricción estática, necesaria para vencer la fricción homóloga, es siempre menor o igual al coeficiente de rozamiento entre los dos objetos (número medido empíricamente y que se encuentra tabulado) multiplicado por la
fuerza normal. La fuerza cinética, en cambio, es igual al coeficiente de rozamiento dinámico, denotado por la letra griega

, por la normal en todo instante.
No se tiene una idea perfectamente clara de la diferencia entre el rozamiento dinámico y el estático, pero se tiende a pensar que el estático es algo mayor que el dinámico, porque al permanecer en reposo ambas superficies pueden aparecer enlaces iónicos, o incluso microsoldaduras entre las superficies, factores que desaparecen en estado de movimiento. Éste fenómeno es tanto mayor cuanto más perfectas son las superficies. Un caso más o menos común es el del gripaje de un motor por estar mucho tiempo parado (no sólo se arruina por una temperatura muy elevada), ya que al permanecer las superficies, del pistón y la camisa, durante largo tiempo en contacto y en reposo, pueden llegar a soldarse entre sí.
Un ejemplo bastante común de fricción dinámica es la ocurrida entre los neumáticos de un auto y el pavimento en un frenado abrupto.
Como comprobación de lo anterior, se realiza el siguiente ensayo, sobre una superficie horizontal se coloca un cuerpo, y le aplica un fuerza horizontal F , muy pequeña en un principio, se puede ver que el cuerpo no se desplaza, la fuerza de rozamiento iguala a la fuerza aplicada y el cuerpo permanece en reposo, en la gráfica se representa en el eje horizontal la fuerza F aplicada, y en el eje vertical la fuerza de rozamiento Fr.
Entre los puntos O y A, ambas fuerzas son iguales y el cuerpo permanece estático; al sobrepasar el punto A el cuerpo súbitamente se comienza a desplazar, la fuerza ejercida en A es la máxima que el cuerpo puede soportar sin deslizarse, se denomina Fe o fuerza estática de fricción; la fuerza necesaria para mantener el cuerpo en movimiento una vez iniciado el desplazamiento es Fd o fuerza dinámica, es menor que la que fue necesaria para iniciarlo (Fe). La fuerza dinámica permanece constante.
Si la fuerza de rozamiento
Fr es proporcional a la normal
N, y a la constante de proporcionalidad se la llama

:
Y permaneciendo la fuerza normal constante, se puede calcular dos coeficientes de rozamiento: el estático y el dinámico como:
donde el
coeficiente de rozamiento estático 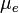
corresponde al de la mayor fuerza que el cuerpo puede soportar inmediatamente antes de iniciar el movimiento y el
coeficiente de rozamiento dinámico 
corresponde a la fuerza necesaria para mantener el cuerpo en movimiento una vez iniciado.
Fricción estática[editar]
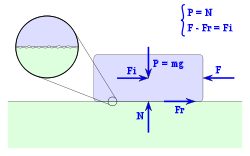
Es la fuerza que se opone al inicio del deslizamiento. Sobre un cuerpo en reposo al que se aplica una fuerza horizontal F, intervienen cuatro fuerzas:
- F: la fuerza aplicada.
- Fr: la fuerza de rozamiento entre la superficie de apoyo y el cuerpo, y que se opone al deslizamiento.
- P: el peso del propio cuerpo, igual a su masa por la aceleración de la gravedad.
- N: la fuerza normal, con la que la superficie reacciona sobre el cuerpo sosteniéndolo.
Dado que el cuerpo está en reposo la fuerza aplicada y la fuerza de rozamiento son iguales, y el peso del cuerpo y la normal:
Se sabe que el peso del cuerpo P es el producto de su masa por la aceleración de la gravedad (g), y que la fuerza de rozamiento es el coeficiente estático por la normal:

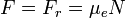
esto es:
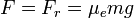
La fuerza horizontal F máxima que se puede aplicar a un cuerpo en reposo es igual al coeficiente de rozamiento estático por su masa y por la aceleración de la gravedad.
Rozamiento dinámico[editar]
Dado un cuerpo en movimiento sobre una superficie horizontal, deben considerarse las siguientes fuerzas:
- Fa: la fuerza aplicada.
- Fr: la fuerza de rozamiento entre la superficie de apoyo y el cuerpo, y que se opone al deslizamiento.
- P: el peso del propio cuerpo, igual a su masa por la aceleración de la gravedad.
- N: la fuerza normal, que la superficie hace sobre el cuerpo sosteniéndolo.
Como equilibrio dinámico, se puede establecer que:
Sabiendo que:

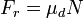
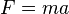
prescindiendo de los signos para tener en cuenta solo las magnitudes, se puede reescribir la segunda ecuación de equilibrio dinámico como:
Es decir, la fuerza de empuje aplicada sobre el cuerpo

es igual a la
fuerza resultante 
menos la fuerza de rozamiento
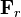
que el cuerpo opone a ser acelerado. De esa esa misma expresión se deduce que la aceleración

que sufre el cuerpo, al aplicarle una fuerza
Fa mayor que la fuerza de rozamiento
Fr con la superficie sobre la que se apoya.
 en un punto
en un punto  en un instante dado dependen sólo de las deformaciones
en un instante dado dependen sólo de las deformaciones 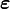 en el mismo punto y no de las deformaciones anteriores (ni el valor de otras magnitudes en un instante anterior). Para un sólido elástico la ecuación constitutiva funcional mente es de la forma:
en el mismo punto y no de las deformaciones anteriores (ni el valor de otras magnitudes en un instante anterior). Para un sólido elástico la ecuación constitutiva funcional mente es de la forma: en un punto
en un punto  en un instante dado dependen sólo de las deformaciones
en un instante dado dependen sólo de las deformaciones 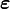 en el mismo punto y no de las deformaciones anteriores (ni el valor de otras magnitudes en un instante anterior). Para un sólido elástico la ecuación constitutiva funcional mente es de la forma:
en el mismo punto y no de las deformaciones anteriores (ni el valor de otras magnitudes en un instante anterior). Para un sólido elástico la ecuación constitutiva funcional mente es de la forma: denota el conjunto de tensores simétricos de segundo orden del espacio euclídeo. Si el sólido es homogéneo el valor de la función anterior no dependerá del segundo argumento.
denota el conjunto de tensores simétricos de segundo orden del espacio euclídeo. Si el sólido es homogéneo el valor de la función anterior no dependerá del segundo argumento. denota el conjunto de tensores simétricos de segundo orden del espacio euclídeo. Si el sólido es homogéneo el valor de la función anterior no dependerá del segundo argumento.
denota el conjunto de tensores simétricos de segundo orden del espacio euclídeo. Si el sólido es homogéneo el valor de la función anterior no dependerá del segundo argumento.

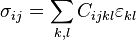

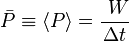
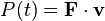

 , son la
, son la 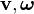 , son la velocidad del punto donde se ha calculado la resultante efectiva y la
, son la velocidad del punto donde se ha calculado la resultante efectiva y la  y sus componentes del movimiento. Se expresa en julios (J). 1 J = 1 kg·m2/s2. Estos son descritos por la
y sus componentes del movimiento. Se expresa en julios (J). 1 J = 1 kg·m2/s2. Estos son descritos por la  de la masa puntual, así:
de la masa puntual, así: 
 o
o  .
.



 , por la normal en todo instante.
, por la normal en todo instante.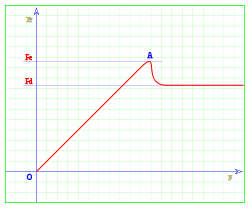
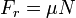
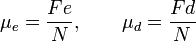
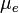 corresponde al de la mayor fuerza que el cuerpo puede soportar inmediatamente antes de iniciar el movimiento y el coeficiente de rozamiento dinámico
corresponde al de la mayor fuerza que el cuerpo puede soportar inmediatamente antes de iniciar el movimiento y el coeficiente de rozamiento dinámico  corresponde a la fuerza necesaria para mantener el cuerpo en movimiento una vez iniciado.
corresponde a la fuerza necesaria para mantener el cuerpo en movimiento una vez iniciado.


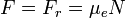
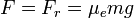
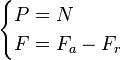
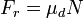
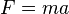

 es igual a la
es igual a la  menos la fuerza de rozamiento
menos la fuerza de rozamiento 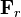 que el cuerpo opone a ser acelerado. De esa esa misma expresión se deduce que la aceleración
que el cuerpo opone a ser acelerado. De esa esa misma expresión se deduce que la aceleración  que sufre el cuerpo, al aplicarle una fuerza Fa mayor que la fuerza de rozamiento Fr con la superficie sobre la que se apoya.
que sufre el cuerpo, al aplicarle una fuerza Fa mayor que la fuerza de rozamiento Fr con la superficie sobre la que se apoya.