Leyes de Newton

Constituyen los cimientos no sólo de la dinámica clásica sino también de la física clásica en general. Aunque incluyen ciertas definiciones y en cierto sentido pueden verse como axiomas, Newton afirmó que estaban basadas en observaciones y experimentos cuantitativos; ciertamente no pueden derivarse a partir de otras relaciones más básicas. La demostración de su validez radica en sus predicciones... La validez de esas predicciones fue verificada en todos y cada uno de los casos durante más de dos siglos.²

En concreto, la relevancia de estas leyes radica en dos aspectos:

• Por un lado, constituyen, junto con la transformación de Galileo, la base de la mecánica clásica;
• Por otro, al combinar estas leyes con la Ley de la gravitación universal, se pueden deducir y explicar las Leyes de Keplersobre el movimiento planetario.

Así, las Leyes de Newton permiten explicar tanto el movimiento de los astros, como los movimientos de los proyectilesartificiales creados por el ser humano, así como toda la mecánica de funcionamiento de las máquinas.

Su formulación matemática fue publicada por Isaac Newton en 1687 en su obra Philosophiae Naturalis Principia Mathematica.³

La dinámica de Newton, también llamada dinámica clásica, sólo se cumple en los sistemas de referencia inerciales (que se mueven a velocidad constante; la Tierra, aunque gire y rote, se trata como tal a efectos de muchos experimentos prácticos). Solo es aplicable a cuerpos cuya velocidad dista considerablemente de la velocidad de la luz (que no se acerquen a los 300.000 km/s); la razón estriba en que cuanto más cerca esté un cuerpo de alcanzar esa velocidad (lo que ocurriría en los sistemas de referencia no-inerciales), más posibilidades hay de que incidan sobre el mismo una serie de fenómenos denominados efectos relativistas o fuerzas ficticias, que añaden términos suplementarios capaces de explicar el movimiento de un sistema cerrado de partículas clásicas que interactúan entre sí. El estudio de estos efectos (aumento de la masa y contracción de la longitud, fundamentalmente) corresponde a la teoría de la relatividad especial, enunciada por Albert Einstein en 1905.

Índice

  [ocultar] 

• 1 Fundamentos teóricos de las leyes
• 2 Las leyes de Newton
  • 2.1 Primera ley de Newton o ley de la inercia
  • 2.2 Segunda ley de Newton o ley de fuerza
  • 2.3 Tercera ley de Newton o principio de acción y reacción
• 3 Generalizaciones
  • 3.1 Generalizaciones relativistas
  • 3.2 Versión débil del principio de acción y reacción
  • 3.3 Teorema de Ehrenfest
• 4 Véase también
• 5 Referencias
  • 5.1 Notas
  • 5.2 Bibliografía

Fundamentos teóricos de las leyeS

El primer concepto que maneja es el de masa, que identifica con «cantidad de materia». La importancia de esta precisión está en que permite prescindir de toda cualidad que no sea física-matemática a la hora de tratar la dinámica de los cuerpos. Con todo, utiliza la idea de éter para poder mecanizar todo aquello no reducible a su concepto de masa.

Newton no asume a continuación que la cantidad de movimiento es el resultado del producto de la masa por la velocidad, y define dos tipos de fuerzas: la vis insita, que es proporcional a la masa y que refleja la inercia de la materia, y la vis impressa (momento de fuerza), que es la acción que cambia el estado de un cuerpo, sea cual sea ese estado; la vis impressa, además de producirse por choque o presión, puede deberse a la vis centrípeta (fuerza centrípeta), una fuerza que lleva al cuerpo hacia algún punto determinado. A diferencia de las otras causas, que son acciones de contacto, la vis centrípeta es una acción a distancia. En esta distingue Newton tres tipos de cantidades de fuerza: una absoluta, otra aceleradora y, finalmente, la motora, que es la que interviene en la ley fundamental del movimiento.

En tercer lugar, precisa la importancia de distinguir entre lo absoluto y relativo siempre que se hable de tiempo, espacio, lugar o movimiento.

En este sentido, Newton, que entiende el movimiento como una traslación de un cuerpo de un lugar a otro, para llegar al movimiento absoluto y verdadero de un cuerpo

compone el movimiento (relativo) de ese cuerpo en el lugar (relativo) en que se lo considera, con el movimiento (relativo) del lugar mismo en otro lugar en el que esté situado, y así sucesivamente, paso a paso, hasta llegar a un lugar inmóvil, es decir, al sistema de referencias de los movimientos absolutos.⁴

De acuerdo con esto, Newton establece que los movimientos aparentes son las diferencias de los movimientos verdaderos y que las fuerzas son causas y efectos de estos. Consecuentemente, la fuerza en Newton tiene un carácter absoluto, no relativo.

Las leyes de Newton[editar]

Primera ley de Newton o ley de la inercia[editar]

La primera ley del movimiento rebate la idea aristotélica de que un cuerpo sólo puede mantenerse en movimiento si se le aplica una fuerza. Newton expone que:

Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él.⁵

La formulación original en latín de Newton de esta ley fue:

Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus illud a viribus impressis cogitur statum suum mutare⁶

Esta ley postúla, por tanto, que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza o una serie de fuerzas cuyo resultante no sea nulo sobre él. Newton toma en cuenta, así, el que los cuerpos en movimiento están sometidos constantemente a fuerzas de roce o fricción, que los frena de forma progresiva, algo novedoso respecto de concepciones anteriores que entendían que el movimiento o la detención de un cuerpo se debía exclusivamente a si se ejercía sobre ellos una fuerza, pero nunca entendiendo como esta a la fricción.

En consecuencia, un cuerpo con movimiento rectilíneo uniforme implica que no existe ninguna fuerza externa neta o, dicho de otra forma; un objeto en movimiento no se detiene de forma natural si no se aplica una fuerza sobre él. En el caso de los cuerpos en reposo, se entiende que su velocidad es cero, por lo que si esta cambia es porque sobre ese cuerpo se ha ejercido una fuerza neta.

La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como Sistemas de referencia inerciales, que son aquellos sistemas de referencia desde los que se observa que un cuerpo sobre el que no actúa ninguna fuerza neta se mueve con velocidad constante.

En realidad, es imposible encontrar un sistema de referencia inercial, puesto que siempre hay algún tipo de fuerzas actuando sobre los cuerpos, pero siempre es posible encontrar un sistema de referencia en el que el problema que estemos estudiando se pueda tratar como si estuviésemos en un sistema inercial. En muchos casos, por ejemplo, suponer a un observador fijo en la Tierra es una buena aproximación de sistema inercial. Lo anterior porque a pesar que la Tierra cuenta con una aceleración traslacional y rotacional estas son del orden de 0.01 m/s^2 y en consecuencia podemos considerar que un sistema de referencia de un observador dentro de la superficie terrestre es un sistema de referencia inercial.

Segunda ley de Newton o ley de fuerza[editar]

La segunda ley del movimiento de Newton dice:

El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.⁷

En las palabras originales de Newton:

Mutationem motus proportionalem esse vi motrici impressæ, & fieri secundum lineam rectam qua vis illa imprimitur.⁶

Esta ley explica qué ocurre si sobre un cuerpo en movimiento (cuya masa no tiene por qué ser constante) actúa una fuerza neta: la fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. En concreto, los cambios experimentados en el momento lineal de un cuerpo son proporcionales a la fuerza motriz y se desarrollan en la dirección de esta; las fuerzas son causas que producen aceleraciones en los cuerpos. Consecuentemente, hay relación entre lacausa y el efecto, la fuerza y la aceleración están relacionadas. Dicho sintéticamente, la fuerza se define simplemente en función del momento que se aplica a un objeto, con lo que dos fuerzas serán iguales si causan la misma tasa de cambio en el momento del objeto.

En términos matemáticos esta ley se expresa mediante la relación:

Donde:

 es el momento lineal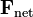

 la fuerza total o fuerza resultante.

Suponiendo que la masa es constante y que la velocidad es muy inferior a la velocidad de la luz⁸ la ecuación anterior se puede reescribir de la siguiente manera:

Sabemos que  es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad.

Consideramos a la masa constante y podemos escribir  aplicando estas modificaciones a la ecuación anterior:

La fuerza es el producto de la masa por la aceleración, que es la ecuación fundamental de la dinámica, donde la constante de proporcionalidad, distinta para cada cuerpo, es su masa de inercia. Veamos lo siguiente, si despejamos m de la ecuación anterior obtenemos que m es la relación que existe entre  y . Es decir la relación que hay entre la fuerza aplicada al cuerpo y la aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a cambiar su aceleración (una gran masa) se dice que tiene mucha inercia. Es por esta razón por la que la masa se define como una medida de la inercia del cuerpo.

Por tanto, si la fuerza resultante que actúa sobre una partícula no es cero, esta partícula tendrá una aceleración proporcional a la magnitud de la resultante y en dirección de ésta. La expresión anterior así establecida es válida tanto para la mecánica clásica como para la mecánica relativista, a pesar de que la definición de momento lineal es diferente en las dos teorías: mientras que la dinámica clásica afirma que la masa de un cuerpo es siempre la misma, con independencia de la velocidad con la que se mueve, la mecánica relativista establece que la masa de un cuerpo aumenta al crecer la velocidad con la que se mueve dicho cuerpo.

De la ecuación fundamental se deriva también la definición de la unidad de fuerza o newton (N). Si la masa y la aceleración valen 1, la fuerza también valdrá 1; así, pues, el newton es la fuerza que aplicada a una masa de un kilogramo le produce una aceleración de 1 m/s². Se entiende que la aceleración y la fuerza han de tener la misma dirección y sentido.

La importancia de esa ecuación estriba sobre todo en que resuelve el problema de la dinámica de determinar la clase de fuerza que se necesita para producir los diferentes tipos de movimiento: rectilíneo uniforme (m.r.u), circular uniforme (m.c.u) y uniformemente acelerado (m.r.u.a).

Si sobre el cuerpo actúan muchas fuerzas, habría que determinar primero el vector suma de todas esas fuerzas. Por último, si se tratase de un objeto que cayese hacia la tierra con una resistencia del aire igual a cero, la fuerza sería su peso, que provocaría una aceleración descendente igual a la de la gravedad.

Tercera ley de Newton o principio de acción y reacción[editar]

Con toda acción ocurre siempre una reacción igual y contraria: quiere decir que las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentido opuesto.⁷

La formulación original de Newton es:

Actioni contrariam semper & æqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse æquales & in partes contrarias dirigi.⁶

La tercera ley de Newton es completamente original (pues las dos primeras ya habían sido propuestas de otras maneras por Galileo, Hooke y Huygens) y hace de las leyes de la mecánica un conjunto lógico y completo.⁹ Expone que por cada fuerza que actúa sobre un cuerpo (empuje), este realiza una fuerza de igual intensidad, pero de sentido contrario sobre el cuerpo que la produjo. Dicho de otra forma, las fuerzas, situadas sobre la misma recta, siempre se presentan en pares de igual magnitud y de dirección, pero con sentido opuesto.

Este principio presupone que la interacción entre dos partículas se propaga instantáneamente en el espacio (lo cual requeriría velocidad infinita), y en su formulación original no es válido para fuerzas electromagnéticas puesto que estas no se propagan por el espacio de modo instantáneo sino que lo hacen a velocidad finita "c".

Es importante observar que este principio relaciona dos fuerzas que no están aplicadas al mismo cuerpo, produciendo en ellos aceleraciones diferentes, según sean sus masas. Por lo demás, cada una de esas fuerzas obedece por separado a la segunda ley. Junto con las anteriores leyes, ésta permite enunciar los principios de conservación del momento lineal y del momento angular.

Generalizaciones[editar]

Después de que Newton formulara las tres famosas leyes, numerosos físicos y matemáticos hicieron contribuciones para darles una forma más general o de más fácil aplicación a sistemas no inerciales o a sistemas con ligaduras. Una de estas primeras generalizaciones fue el principio de d'Alembert de 1743 que era una forma válida para cuando existieran ligaduras que permitía resolver las ecuaciones sin necesidad de calcular explícitamente el valor de las reacciones asociadas a dichas ligaduras.

Por la misma época, Lagrange encontró una forma de las ecuaciones de movimiento válida para cualquier sistema de referencia inercial o no-inercial sin necesidad de introducir fuerzas ficticias. Ya que es un hecho conocido que las Leyes de Newton, tal como fueron escritas, sólo son válidas a los sistemas de referencia inerciales, o más precisamente, para aplicarlas a sistemas no-inerciales, requieren la introducción de las llamadas fuerzas ficticias, que se comportan como fuerzas pero no están provocadas directamente por ninguna partícula material o agente concreto, sino que son un efecto aparente del sistema de referencia no inercial.

Más tarde la introducción de la teoría de la relatividad obligó a modificar la forma de la segunda ley de Newton (ver (2c)), y la mecánica cuántica dejó claro que las leyes de Newton o la relatividad general sólo son aproximaciones al comportamiento dinámico en escalas macroscópicas. También se han conjeturado algunas modificaciones macroscópicas y no-relativistas, basadas en otros supuestos como la dinámica MOND.