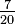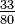La temperatura de un
gas ideal
monoatómico es una medida relacionada con la
energía cinéticapromedio de sus moléculas al moverse. En esta animación, se muestra a escala la relación entre el
tamaño de los átomos de
helio respecto a su espaciado bajo una presión de 1950
atmósferas. Estos átomos, a temperatura ambiente, muestran una velocidad media que en esta animación se ha reducido dos
billones de veces. De todas maneras, en un instante determinado, un átomo particular de helio puede moverse mucho más rápido que esa velocidad media mientras que otro puede permanecer prácticamente inmóvil.
La
temperatura es una
magnitud referida a las nociones comunes de
caliente, tibio o
frío que puede ser medida con un
termómetro. En física, se define como una
magnitud escalar relacionada con la
energía internade un sistema termodinámico, definida por el
principio cero de la termodinámica. Más específicamente, está relacionada directamente con la parte de la energía interna conocida como «energía cinética», que es la energía asociada a los movimientos de las partículas del sistema, sea en un sentido traslacional, rotacional, o en forma de
vibraciones. A medida de que sea mayor la energía cinética de un sistema, se observa que éste se encuentra más «caliente»; es decir, que su temperatura es mayor.
En el caso de un sólido, los movimientos en cuestión resultan ser las
vibraciones de las partículas en sus sitios dentro del sólido. En el caso de un
gas ideal monoatómico se trata de los movimientos traslacionales de sus partículas (para los gases multiatómicos los movimientos rotacional y vibracional deben tomarse en cuenta también).
El desarrollo de técnicas para la medición de la temperatura ha pasado por un largo proceso histórico, ya que es necesario darle un valor numérico a una idea intuitiva como es lo frío o lo caliente.
La temperatura se mide con
termómetros, los cuales pueden ser calibrados de acuerdo a una multitud de escalas que dan lugar a unidades de medición de la temperatura. En el
Sistema Internacional de Unidades, la unidad de temperatura es el
kelvin (K), y la escala correspondiente es la
escala Kelvin o escala absoluta, que asocia el valor «cero kelvin» (0 K) al «
cero absoluto», y se gradúa con un tamaño de grado igual al del
grado Celsius. Sin embargo, fuera del ámbito científico el uso de otras escalas de temperatura es común. La escala más extendida es la escala
Celsius, llamada «centígrada»; y, en mucha menor medida, y prácticamente solo en los
Estados Unidos, la escala
Fahrenheit. También se usa a veces la escala
Rankine (°R) que establece su punto de referencia en el mismo punto de la escala
Kelvin, el
cero absoluto, pero con un tamaño de grado igual al de la Fahrenheit, y es usada únicamente en
Estados Unidos, y solo en algunos campos de la
ingeniería.
Nociones generales[editar]
La temperatura es una propiedad física que se refiere a las nociones comunes de calor o ausencia de calor, sin embargo su significado formal en termodinámica es más complejo. Termodinámicamente se habla de la velocidad promedio o la energía cinética (movimiento) de las partículas de las moléculas, siendo de esta manera, a temperaturas altas, las velocidad de las partículas es alta, en el cero absoluto (0°K) las partículas no tienen movimiento. A menudo el calor o el frío percibido por las personas tiene más que ver con la
sensación térmica (ver más abajo), que con la temperatura real. Fundamentalmente, la temperatura es una propiedad que poseen los sistemas físicos a nivel macroscópico, la cual tiene una causa a nivel microscópico, que es la energía promedio por la partícula. Y actualmente, al contrario de otras cantidades termodinámicas como el calor o la entropía, cuyas definiciones microscópicas son válidas muy lejos del
equilibrio térmico, la temperatura solo puede ser medida en el equilibrio, precisamente porque se define como un promedio.
La temperatura está íntimamente relacionada con la
energía interna y con la
entalpía de un sistema: a mayor temperatura mayores serán la energía interna y la entalpía del sistema.
La temperatura es una
propiedad intensiva, es decir, que no depende del tamaño del sistema, sino que es una propiedad que le es inherente y no depende ni de la cantidad de sustancia ni del material del que este compuesto.
Ley cero de la termodinámica[editar]

Un
termómetrodebe alcanzar el equilibrio térmico antes de que su medición sea correcta.
Antes de dar una definición formal de temperatura, es necesario entender el concepto de
equilibrio térmico. Si dos partes de un sistema entran en contacto térmico es probable que ocurran cambios en las propiedades de ambas. Estos cambios se deben a la transferencia de calor entre las partes. Para que un sistema esté en equilibrio térmico debe llegar al punto en que ya no hay intercambio neto de calor entre sus partes, además ninguna de las propiedades que dependen de la temperatura debe variar.
Una definición de temperatura se puede obtener de la
Ley cero de la termodinámica, que establece que si dos sistemas A y B están en equilibrio térmico, con un tercer sistema C, entonces los sistemas A y B estarán en equilibrio térmico entre sí.
1 Este es un hecho empírico más que un resultado teórico. Ya que tanto los sistemas A, B, y C están todos en equilibrio térmico, es razonable decir que comparten un valor común de alguna propiedad física. Llamamos a esta propiedad
temperatura.
Sin embargo, para que esta definición sea útil es necesario desarrollar un instrumento capaz de dar un significado cuantitativo a la noción cualitativa de ésa propiedad que presuponemos comparten los sistemas A y B. A lo largo de la historia se han hecho numerosos intentos, sin embargo en la actualidad predominan el sistema inventado por
Anders Celsius en
1742 y el inventado por
William Thomson (más conocido como lord Kelvin) en
1848.
Segunda ley de la termodinámica[editar]
También es posible definir la temperatura en términos de la
segunda ley de la termodinámica, la cual dice que la
entropía de todos los sistemas, o bien permanece igual o bien aumenta con el tiempo, esto se aplica al Universo entero como sistema termodinámico.
2 La entropía es una medida del desorden que hay en un sistema. Este concepto puede ser entendido en términos estadísticos, considere una serie de tiros de monedas. Un sistema perfectamente ordenado para la serie, sería aquel en que solo cae cara o solo cae cruz. Sin embargo, existen múltiples combinaciones por las cuales el resultado es un desorden en el sistema, es decir que haya una fracción de caras y otra de cruces. Un sistema desordenado podría ser aquel en el que hay 90 % de caras y 10 % de cruces, o 60 % de caras y 40 % de cruces. Sin embargo es claro que a medida que se hacen más tiros, el número de combinaciones posibles por las cuales el sistema se desordena es mayor; en otras palabras el sistema evoluciona naturalmente hacia un estado de desorden máximo es decir 50 % caras 50 % cruces de tal manera que cualquier variación fuera de ese estado es altamente improbable.
Para dar la definición de temperatura con base en la segunda ley, habrá que introducir el concepto de
máquina térmica la cual es cualquier dispositivo capaz de transformar calor en
trabajo mecánico. En particular interesa conocer el planteamiento teórico de la
máquina de Carnot, que es una máquina térmica de construcción teórica, que establece los límites teóricos para la eficiencia de cualquier máquina térmica real.

Aquí se muestra el
ciclo de la máquina térmica descrita por Carnot, el
calor entra al sistema a través de una temperatura inicial (aquí se muestra como
TH) y fluye a través del mismo obligando al sistema a ejercer un trabajo sobre sus alrededores, y luego pasa al medio frío, el cual tiene una temperatura final (
TC).
En una máquina térmica cualquiera, el trabajo que esta realiza corresponde a la diferencia entre el calor que se le suministra y el calor que sale de ella. Por lo tanto, la eficiencia es el trabajo que realiza la máquina dividido entre el calor que se le suministra:
 (1)
(1)
Donde Wci es el trabajo hecho por la máquina en cada ciclo. Se ve que la eficiencia depende solo de Qi y de Qf. Ya que Qi y Qf corresponden al calor transferido a las temperaturas Ti y Tf, es razonable asumir que ambas son funciones de la temperatura:
 (2)
(2)
Sin embargo, es posible utilizar a conveniencia, una escala de temperatura tal que
 (3)
(3)
Sustituyendo la ecuación (3) en la (1) relaciona la eficiencia de la máquina con la temperatura:
 (4)
(4)
Hay que notar que para
Tf = 0 K la eficiencia se hace del 100 %, temperaturas inferiores producen una eficiencia aún mayor que 100 %. Ya que la
primera ley de la termodinámica prohíbe que la eficiencia sea mayor que el 100 %, esto implica que la mínima temperatura que se puede obtener en un sistema microscópico es de 0 K. Reordenando la ecuación (4) se obtiene:
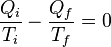 (5)
(5)
Aquí el signo negativo indica la salida de calor del sistema. Esta relación sugiere la existencia de una
función de estado S definida por:
 (6)
(6)
Donde el subíndice indica un proceso reversible. El cambio de esta función de estado en cualquier ciclo es cero, tal como es necesario para cualquier función de estado. Esta función corresponde a la entropía del sistema, que fue descrita anteriormente. Reordenando la ecuación siguiente para obtener una definición de temperatura en términos de la entropía y el
calor:
 (7)
(7)
Para un sistema en que la entropía sea una función de su energía interna E, su temperatura está dada por:
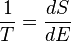 (8)
(8)
Esto es, el recíproco de la temperatura del sistema es la razón de cambio de su entropía con respecto a su energía.
Unidades de temperatura[editar]
Las escalas de medición de la temperatura se dividen fundamentalmente en dos tipos, las relativas y las absolutas. Los valores que puede adoptar la temperatura en cualquier escala de medición, no tienen un nivel máximo, sino un nivel mínimo: el
cero absoluto.
3 Mientras que las escalas absolutas se basan en el cero absoluto, las relativas tienen otras formas de definirse.
- Grado Celsius (°C). Para establecer una base de medida de la temperatura Anders Celsius utilizó (en 1742) los puntos de fusión y ebullición del agua. Se considera que una mezcla de hielo y agua que se encuentra en equilibrio con aire saturado a 1 atm está en el punto de fusión. Una mezcla de agua y vapor de agua (sin aire) en equilibrio a 1 atm de presión se considera que está en el punto de ebullición. Celsius dividió el intervalo de temperatura que existe entre éstos dos puntos en 100 partes iguales a las que llamó grados centígrados °C. Sin embargo, en 1948 fueron renombrados grados Celsius en su honor; así mismo se comenzó a utilizar la letra mayúscula para denominarlos.
- En 1954 la escala Celsius fue redefinida en la Décima Conferencia de Pesos y Medidas en términos de un sólo punto fijo y de la temperatura absoluta del cero absoluto. El punto escogido fue el punto triple del agua que es el estado en el que las tres fases del agua coexisten en equilibrio, al cual se le asignó un valor de 0,01 °C. La magnitud del nuevo grado Celsius se define a partir del cero absoluto como la fracción 1/273,16 del intervalo de temperatura entre el punto triple del agua y el cero absoluto. Como en la nueva escala los puntos de fusión y ebullición del agua son 0,00 °C y 100,00 °C respectivamente, resulta idéntica a la escala de la definición anterior, con la ventaja de tener una definición termodinámica.
Las escalas que asignan los valores de la temperatura en dos puntos diferentes se conocen como escalas a dos puntos. Sin embargo en el estudio de la termodinámica es necesario tener una escala de medición que no dependa de las propiedades de las sustancias. Las escalas de éste tipo se conocen comoescalas absolutas o escalas de temperatura termodinámicas.
Con base en el esquema de notación introducido en 1967, en la Conferencia General de Pesos y Medidas (CGPM), el símbolo de grado se eliminó en forma oficial de la unidad de temperatura absoluta.
Sistema Internacional de Unidades (SI)[editar]
- Kelvin (K) El kelvin es la unidad de medida del SI. La escala kelvin absoluta parte del cero absoluto y define la magnitud de sus unidades, de tal forma que elpunto triple del agua es exactamente a 273,16 K.3
Aclaraciones: No se le antepone la palabra grado ni el símbolo º. Cuando se escribe la palabra completa, «kelvin», se hace con minúscula, salvo que sea principio de párrafo.
Sistema anglosajón de unidades[editar]
- Rankine (R o Ra). Escala con intervalos de grado equivalentes a la escala Fahrenheit, cuyo origen está en -459,67 °F. En desuso.
Conversión de temperaturas[editar]
Las siguientes fórmulas asocian con precisión las diferentes escalas de temperatura:
| Kelvin | Grado Celsius | Grado Fahrenheit | Rankine | Grado Réaumur | Grado Rømer | Grado Newton | Grado Delisle |
|---|
| Kelvin |  |  |   |   | K = Re  + 273,15 + 273,15 | K = (Ro - 7,5) + 273,15 + 273,15 | K = N 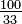 + 273,15 + 273,15 | K = 373,15 - De  |
| Grado Celsius |  |  | C = (F - 32)  | C = (Ra - 491,67)  | C = Re  | C = (Ro - 7,5)  | C = N 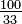 | C = 100 - De |
| Grado Fahrenheit |   - 459,67 - 459,67 | F = C  + 32 + 32 |  |  | F = Re  + 32 + 32 | F = (Ro - 7,5)  + 32 + 32 | F = N  + 32 + 32 | F = 121 - De 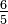 |
| Rankine |   | Ra = (C + 273,15)  |  |  | Ra = Re  + 491,67 + 491,67 | Ra = (Ro - 7,5) + 491,67 + 491,67 | Ra = N  + 491,67 + 491,67 | Ra = 171,67 - De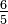 |
| Grado Réaumur |  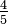 | Re = C 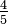 | Re = (F - 32)  | Re = (Ra - 491,67)  |  | Re = (Ro - 7,5) | Re = N  | Re = 80 - De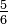 |
| Grado Rømer | Ro =(K - 273,15)  +7,5 +7,5 | Ro = C  +7,5 +7,5 | Ro = (F - 32)  +7,5 +7,5 | Ro = Ra - 491,67  +7,5 +7,5 | Ro = Re 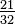 +7,5 +7,5 |  | Ro = N  +7,5 +7,5 | Ro = 60 - De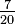 |
| Grado Newton | N = (K - 273,15)  | N = C  | N = (F - 32)  | N = (Ra - 491,67)  | N = Re 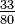 | N = (Ro - 7,5)  |  | N = 33 - De  |
| Grado Delisle | De = (373,15 - K)  | De = (100 - C)  | De = (121 - F) 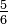 | De = (580,67 - Ra) 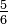 | De = (80 - Re) 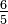 | De = (60 - Ro)  | De = (33 - N)  |  |
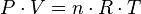
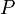 =
=  =
= 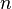 =
=  =
= 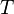 =
= 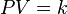

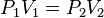


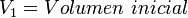

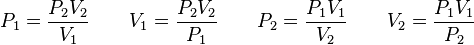



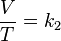
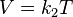
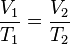
 = Volumen inicial
= Volumen inicial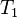 = Temperatura inicial
= Temperatura inicial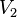 = Volumen final
= Volumen final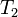 = Temperatura final
= Temperatura final
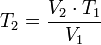
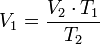


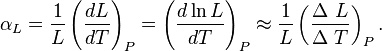
 , es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura
, es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura 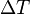 a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:![L_f = L_0 [1 +\alpha_L (T_f - T_0)]\;](http://upload.wikimedia.org/math/4/d/8/4d8d9e521d59aa36de0d776706db3b16.png)
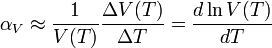

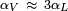 , es decir, el coeficiente de dilatación volumétrico es numéricamente unas 3 veces el coeficiente de dilatación lineal de una barra del mismo material.
, es decir, el coeficiente de dilatación volumétrico es numéricamente unas 3 veces el coeficiente de dilatación lineal de una barra del mismo material.
![A_f = A_0 [1 +\gamma_A (T_f - T_0)]\;](http://upload.wikimedia.org/math/8/4/4/84444b9c6e865aaf0b6d1376be7a9a6b.png)



 (1)
(1) (2)
(2) (3)
(3) (4)
(4)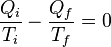 (5)
(5) (6)
(6) (7)
(7)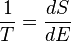 (8)
(8)




 + 273,15
+ 273,15 + 273,15
+ 273,15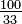 + 273,15
+ 273,15



 - 459,67
- 459,67

 + 32
+ 32 + 32
+ 32 + 32
+ 32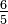




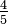




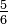
 +7,5
+7,5 +7,5
+7,5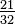 +7,5
+7,5
 +7,5
+7,5