Casos específicos
Circuito serie RL
Se supone que por el circuito de la figura 8a circula una corriente:
Como 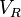 está en fase y
está en fase y 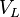 adelantada 90º respecto a dicha corriente, se tendrá:
adelantada 90º respecto a dicha corriente, se tendrá:
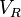 está en fase y
está en fase y 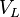 adelantada 90º respecto a dicha corriente, se tendrá:
adelantada 90º respecto a dicha corriente, se tendrá:
Sumando fasorialmente ambas tensiones se obtiene la total V:
donde, y de acuerdo con el diagrama fasorial de la figura 8b, V es el módulo de la tensión total:
La expresión  representa la oposición que ofrece el circuito al paso de la corriente alterna, a la que se denomina impedancia y se representa Z:
representa la oposición que ofrece el circuito al paso de la corriente alterna, a la que se denomina impedancia y se representa Z:
 representa la oposición que ofrece el circuito al paso de la corriente alterna, a la que se denomina impedancia y se representa Z:
representa la oposición que ofrece el circuito al paso de la corriente alterna, a la que se denomina impedancia y se representa Z:
En forma polar:
con lo que la impedancia puede considerarse como una magnitud compleja, cuyo valor, de acuerdo con el triángulo de la figura 9, es:
Obsérvese que la parte real resulta ser la componente resistiva y la parte imaginaria la inductiva.
Circuito serie RC
Se supone que por el circuito de la figura 10a circula una corriente:
Como 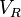 está en fase y
está en fase y  retrasada 90º respecto a dicha corriente, se tendrá:
retrasada 90º respecto a dicha corriente, se tendrá:
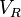 está en fase y
está en fase y  retrasada 90º respecto a dicha corriente, se tendrá:
retrasada 90º respecto a dicha corriente, se tendrá:
La tensión total V será igual a la suma fasorial de ambas tensiones,
Y de acuerdo con su diagrama fasorial (figura 10b) se tiene:
Al igual que en el apartado anterior la expresión  es el módulo de la impedancia, ya que
es el módulo de la impedancia, ya que
 es el módulo de la impedancia, ya que
es el módulo de la impedancia, ya que
lo que significa que la impedancia es una magnitud compleja cuyo valor, según el triángulo de la figura 11, es:
Obsérvese que la parte real resulta ser la componente resistiva y la parte imaginaria, ahora con signo negativo, la capacitiva.
Circuito serie RLC
Razonado de modo similar en el circuito serie RLC de la figura 12 se llega a la conclusión de que la impedancia Z tiene un valor de:
siendo φ

En el diagrama se ha supuesto que el circuito era inductivo ( ), pero en general se pueden dar los siguientes casos:
), pero en general se pueden dar los siguientes casos:
 ), pero en general se pueden dar los siguientes casos:
), pero en general se pueden dar los siguientes casos: : circuito inductivo, la intensidad queda retrasada respecto de la tensión (caso de la figura 12, donde φ es el ángulo de desfase).
: circuito inductivo, la intensidad queda retrasada respecto de la tensión (caso de la figura 12, donde φ es el ángulo de desfase). : circuito capacitivo, la intensidad queda adelantada respecto de la tensión.
: circuito capacitivo, la intensidad queda adelantada respecto de la tensión. : circuito resistivo, la intensidad queda en fase con la tensión (en este caso se dice que hay resonancia).
: circuito resistivo, la intensidad queda en fase con la tensión (en este caso se dice que hay resonancia).
Circuito serie general
Sean n impedancias en serie como las mostradas en la figura 13a, a las que se le aplica una tensión alterna V entre los terminales A y B lo que originará una corriente I. De acuerdo con la ley de Ohm:
donde  es la impedancia equivalente de la asociación (figura 13c), esto es, aquella que conectada la misma tensión lterna,
es la impedancia equivalente de la asociación (figura 13c), esto es, aquella que conectada la misma tensión lterna,  , demanda la misma intensidad,
, demanda la misma intensidad,  . Del mismo modo que para una asociación serie de resistencias, se puede demostrar que
. Del mismo modo que para una asociación serie de resistencias, se puede demostrar que
 es la impedancia equivalente de la asociación (figura 13c), esto es, aquella que conectada la misma tensión lterna,
es la impedancia equivalente de la asociación (figura 13c), esto es, aquella que conectada la misma tensión lterna,  , demanda la misma intensidad,
, demanda la misma intensidad,  . Del mismo modo que para una asociación serie de resistencias, se puede demostrar que
. Del mismo modo que para una asociación serie de resistencias, se puede demostrar que
lo que implica:
y
Circuito paralelo general
Del mismo modo que en el apartado anterior, se consideran "n" impedancias en paralelo como las mostradas en la figura 13b, a las que se le aplica una tensión alterna "V" entre los terminales A y B lo que originará una corriente "I". De acuerdo con la ley de Ohm:
y del mismo modo que para una asociación paralelo de resistencias, se puede demostrar que



























No hay comentarios.:
Publicar un comentario