Onda longitudinal
Una onda longitudinal es una onda mecánica en la que el movimiento de oscilación de las partículas del medio es paralelo a la dirección de propagación de la onda. Las ondas longitudinales reciben también el nombre de ondas de presión u ondas de compresión. Algunos ejemplos de ondas longitudinales son el sonido y las ondas sísmicas de tipo P generadas en un terremoto.
En teoría de campos también pueden existir ondas no mecánicas de tipo longitudinal, aunque las ondas electromagnéticas son siempre ondas transversales nunca longitudinales debido a que el fotón es una partícula sin masa.
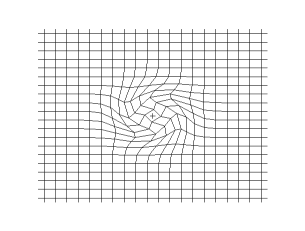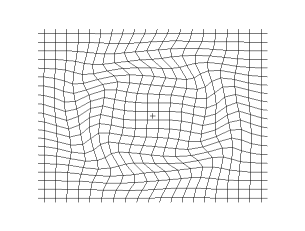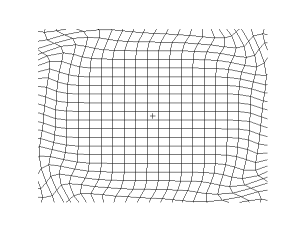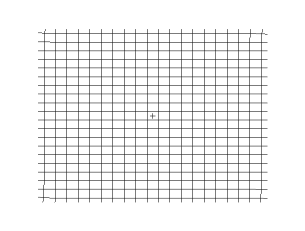
La figura ilustra el caso de una onda sonora. Si el centro de la figura es un foco puntual generador de la onda, los frentes de onda se desplazan alejándose del foco, transmitiendo el sonido a través del medio de propagación, por ejemplo aire. Por otro lado, cada partícula de un frente de onda cualquiera oscila en dirección de la propagación, esto es, inicialmente empujada en la acción por efecto del incremento de presión provocado por el foco, retornando a su posición anterior por efecto de la disminución de presión provocada por su desplazamiento, por esa razón las ondas sonoras son ondas longitudinales. Estas necesitan de un medio material(solido, liquido o gas).
Sonido
 El sonido humanamente audible consiste en ondas sonoras que se producen cuando las oscilaciones de la presión del aire, son convertidas en ondas mecánicas en el oído humano y percibidas por el cerebro. La propagación del sonido es similar en los fluidos, donde el sonido toma la forma de fluctuaciones de presión.1 En los cuerpos sólidos la propagación del sonido involucra variaciones del estado tensional del medio.
El sonido humanamente audible consiste en ondas sonoras que se producen cuando las oscilaciones de la presión del aire, son convertidas en ondas mecánicas en el oído humano y percibidas por el cerebro. La propagación del sonido es similar en los fluidos, donde el sonido toma la forma de fluctuaciones de presión.1 En los cuerpos sólidos la propagación del sonido involucra variaciones del estado tensional del medio.
La propagación del sonido involucra transporte de energía sin transporte de materia, en forma de ondas mecánicas que se propagan a través de un medio elástico sólido, líquido o gaseoso. Entre los más comunes se encuentran el aire y el agua. No se propagan en el vacío, al contrario que las ondas electromagnéticas. Si las vibraciones se producen en la misma dirección en la que se propaga el sonido, se trata de una onda longitudinal y si las vibraciones son perpendiculares a la dirección de propagación es una onda transversal.
La fonética acústica concentra su interés especialmente en los sonidos del habla: cómo se generan, cómo se perciben, y cómo se pueden describir gráfica o cuantitativamente.
Física del sonido
La física del sonido es estudiada por la acústica, que trata tanto de la propagación de las ondas sonoras en los diferentes tipos de medios continuos como la interacción de estas ondas sonoras con los cuerpos físicos.
Propagación del sonido
Ciertas características de los fluidos y de los sólidos influyen en la onda de sonido. Es por eso que el sonido se propaga en los sólidos y en los líquidos con mayor rapidez que en los gases. En general cuanto mayor sea lacompresibilidad (1/K) del medio tanto menor es la velocidad del sonido. También la densidad es un factor importante en la velocidad de propagación, en general cuanto menor sea la densidad (ρ), a igualdad de todo lo demás, mayor es la velocidad de la propagación del sonido. La velocidad del sonido se relaciona con esas magnitudes mediante:
En los gases, la temperatura influye tanto la compresibilidad como la densidad, de tal manera que el factor de importancia suele ser la calentura actual
La propagación del sonido está sujeta a algunos condicionales. Así la transmisión de sonido requiere la existencia de un medio material donde la vibración de las moléculas es percibida como una onda sonora. En la propagación en medios compresibles como el aire, la propagación implica que en algunas zonas las moléculas de aire, al vibrar se juntan (zonas de compresión) y en otras zonas se alejan (zonas de rarefacción), esta alteración de distancias entre las moléculas de aire es lo que produce el sonido. En fluidos altamente incompresibles como los líquidos las distancias se ven muy poco afectadas pero se manifiesta en forma de ondas de presión. La velocidad de propagación de las ondas sonoras en un medio depende de la distancia promedio entre las partículas de dicho medio, por tanto, es en general mayor en los sólidos que en los líquidos y en estos, a su vez, que en los gases. En el vacío no puede propagarse el sonido, nótese que por tanto las explosiones realmente no son audibles en el espacio exterior.
Las ondas sonoras se producen cuando un cuerpo vibra rápidamente. La frecuencia es el número de vibraciones u oscilaciones completas que efectúan por segundo. Los sonidos producidos son audibles por un ser humano promedio si la frecuencia de oscilación está comprendida entre 20 Hz y 20000 Hz. Por encima de esta última frecuencia se tiene un ultrasonido no audible por los seres humanos, aunque algunos animales pueden oír ultrasonidos inaudibles por los seres humanos. La intensidad de un sonido está relacionada con el cuadrado de la amplitud de presión de la onda sonora. Un sonido grave corresponde a onda sonora con frecuencia baja mientras que los sonidos agudos se corresponden con frecuencias más altas.
Magnitudes físicas del sonido
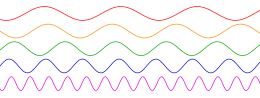
Como todo movimiento ondulatorio, el sonido puede representarse mediante la Transformada de Fourier como una suma de curvas sinusoides, tonos puros, con un factor de amplitud, que se pueden caracterizar por las mismas magnitudes y unidades de medida que a cualquier onda de frecuencia bien definida: Longitud de onda (λ), frecuencia (f) o inversa del período (T), amplitud (relacionada con el volumen y la potencia acústica) y fase. Esta descomposición simplifica el estudio de sonidos complejos ya que permite estudiar cada componente frecuencial independientemente y combinar los resultados aplicando el principio de superposición, que se cumple porque la alteración que provoca un tono no modifica significativamente las propiedades del medio.
La caracterización de un sonido arbitrariamente complejo implica analizar:
- Potencia acústica: El nivel de potencia acústica (PWL Power Wattage Level) es la cantidad de energía radiada al medio en forma de ondas por unidad de tiempo por una fuente determinada. La unidad en que se mide el vatio y su símbolo W. La potencia acústica depende de la amplitud.
- Espectro de frecuencias: la distribución de dicha energía entre las diversas ondas componentes.
Velocidad del sonido
- El sonido tiene una velocidad de 331,5 m/s cuando: la temperatura es de 0 °C, la presión atmosférica es de 1 atm (nivel del mar) y se presenta una humedad relativa del aire de 0 % (aire seco). Aunque depende muy poco de la presión del aire.
- La velocidad del sonido depende del tipo de material. Cuando el sonido se desplaza en los sólidos tiene mayor velocidad que en los líquidos, y en los líquidos es más veloz que en los gases. Esto se debe a que las partículas en los sólidos están más cercanas.
La velocidad del sonido en el aire se puede calcular en relación a la temperatura de la siguiente manera:
Donde:


![T\ [{}^\circ\mbox{C}]](http://upload.wikimedia.org/math/4/0/0/400c8461c703525d457e4fcdf7cde531.png) , es la temperatura en grados Celsius.
, es la temperatura en grados Celsius.
Si la temperatura ambiente es de 15 °C, la velocidad de propagación del sonido es 340 m/s (1224 km/h ).
Reverberación
La reverberación es la suma total de las reflexiones del sonido que llegan al lugar del oyente en diferentes momentos del tiempo. Auditivamente se caracteriza por una prolongación, a modo de "cola sonora", que se añade al sonido original. La duración y la coloración tímbrica de esta cola dependen de: La distancia entre el oyente y la fuente sonora; la naturaleza de las superficies que reflejan el sonido. En situaciones naturales hablamos de sonido directo para referirnos al sonido que se transmite directamente desde la fuente sonora hasta nosotros (o hasta el mecanismo de captación que tengamos). Por otra parte, el sonido reflejado es el que percibimos después de que haya rebotado en las superficies que delimitan el recinto acústico, o en los objetos que se encuentren en su trayectoria. Evidentemente, la trayectoria del sonido reflejado siempre será más larga que la del sonido directo, de manera que -temporalmente- escuchamos primero el sonido directo, y unos instantes más tarde escucharemos las primeras reflexiones; a medida que transcurre el tiempo las reflexiones que nos llegan son cada vez de menor intensidad, hasta que desaparecen. Nuestra sensación, no obstante, no es la de escuchar sonidos separados, ya que el cerebro los integra en un único precepto, siempre que las reflexiones lleguen con una separación menor de unos 50 milisegundos. Esto es lo que se denomina efecto Haas o efecto de precedencia.
Resonancia
Es el fenómeno que se produce cuando dos cuerpos tienen la misma frecuencia de vibración, uno de los cuales empieza a vibrar al recibir las ondas sonoras emitidas por el otro.
Para entender el fenómeno de la resonancia existe un ejemplo muy sencillo. Supóngase que se tiene un tubo con agua y muy cerca de él (sin entrar en contacto) tenemos un diapasón, si golpeamos el diapasón con un metal, mientras echan agua en el tubo, cuando el agua alcance determinada altura el sonido será más fuerte; esto se debe a que la columna de agua contenida en el tubo se pone a vibrar con la misma frecuencia que la que tiene el diapasón, lo que evidencia por qué las frecuencias se refuerzan y en consecuencia aumenta la intensidad del sonido.
Un ejemplo es el efecto de afinar las cuerdas de la guitarra, puesto que al afinar, lo que se hace es igualar las frecuencias, es decir poner en resonancia el sonido de las cuerdas.


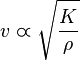






 ..........(1)
..........(1) 
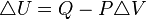 ,
,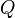 =
= 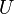 =
= 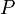 =
=  =
= 
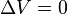 . Esto implica que el proceso no realiza
. Esto implica que el proceso no realiza 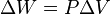 ,
,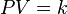
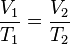 o
o  .
.

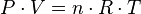
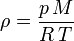
 es la
es la  es la presión del gas,
es la presión del gas,  su
su 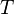 la
la 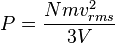 (gas ideal)
(gas ideal)